Kakuro Extension

If you solved problem like this, forget it.Because you need to use a completely different algorithm to solve the following one.
Kakuro puzzle is played on a grid of "black" and "white" cells. Apart from the top row and leftmost column which are entirely black, the grid has some amount of white cells which form "runs" and some amount of black cells. "Run" is a vertical or horizontal maximal one-lined block of adjacent white cells. Each row and column of the puzzle can contain more than one "run". Every white cell belongs to exactly two runs — one horizontal and one vertical run. Each horizontal "run" always has a number in the black half-cell to its immediate left, and each vertical "run" always has a number in the black half-cell immediately above it. These numbers are located in "black" cells and are called "clues".The rules of the puzzle are simple:

1.place a single digit from 1 to 9 in each "white" cell
2.for all runs, the sum of all digits in a "run" must match the clue associated with the "run"

Given the grid, your task is to find a solution for the puzzle.
　　　　　　　　 　　　　　
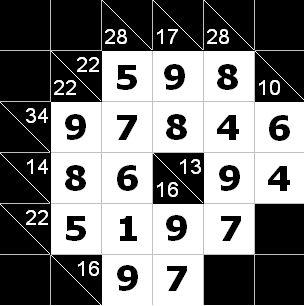
　　　　　　　　Picture of the first sample input　　　　　　　　　　　　Picture of the first sample output

The first line of input contains two integers n and m (2 ≤ n,m ≤ 100) — the number of rows and columns correspondingly. Each of the next n lines contains descriptions of m cells. Each cell description is one of the following 7-character strings:

.......— "white" cell;
XXXXXXX— "black" cell with no clues;
AAA\BBB— "black" cell with one or two clues. AAA is either a 3-digit clue for the corresponding vertical run, or XXX if there is no associated vertical run. BBB is either a 3-digit clue for the corresponding horizontal run, or XXX if there is no associated horizontal run.
The first row and the first column of the grid will never have any white cells. The given grid will have at least one "white" cell.It is guaranteed that the given puzzle has at least one solution.

Print n lines to the output with m cells in each line. For every "black" cell print '_' (underscore), for every "white" cell print the corresponding digit from the solution. Delimit cells with a single space, so that each row consists of 2m-1 characters.If there are many solutions, you may output any of them.

6 6
XXXXXXX XXXXXXX 028\XXX 017\XXX 028\XXX XXXXXXX
XXXXXXX 022\022 ....... ....... ....... 010\XXX
XXX\034 ....... ....... ....... ....... .......
XXX\014 ....... ....... 016\013 ....... .......
XXX\022 ....... ....... ....... ....... XXXXXXX
XXXXXXX XXX\016 ....... ....... XXXXXXX XXXXXXX
5 8
XXXXXXX 001\XXX 020\XXX 027\XXX 021\XXX 028\XXX 014\XXX 024\XXX
XXX\035 ....... ....... ....... ....... ....... ....... .......
XXXXXXX 007\034 ....... ....... ....... ....... ....... .......
XXX\043 ....... ....... ....... ....... ....... ....... .......
XXX\030 ....... ....... ....... ....... ....... ....... XXXXXXX

_ _ _ _ _ _
_ _ 5 8 9 _
_ 7 6 9 8 4
_ 6 8 _ 7 6
_ 9 2 7 4 _
_ _ 7 9 _ _
_ _ _ _ _ _ _ _
_ 1 9 9 1 1 8 6
_ _ 1 7 7 9 1 9
_ 1 3 9 9 9 3 9
_ 6 7 2 4 9 2 _

NotOnlySuccess@HDU

HDOJ Monthly Contest – 2010.03.06