
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Inverse
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 130 Accepted Submission(s): 3
Problem Description
YY and LMY both love mathematics. One day LMY wrote down an integer 3 and two polynomials 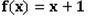 and
and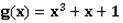 on a piece of paper.
on a piece of paper.
YY noticed that 3 is a prime. Besides, he found that f(x) has a degree strictly less than g(x). And all coefficients of the two polynomials are between 0 and 2,
inclusively. His most important discovery is, that there is a polynomial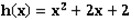 , such that
, such that
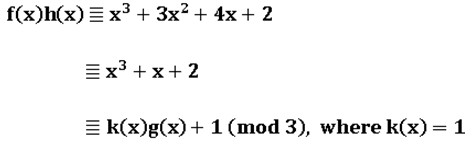
Then YY added a restriction: all coefficients of h(x) must be between 0 and 2 inclusively, and its degree must be less than g(x). Finally, he found that the polynomial
h(x) with such properties is unique.
The property that a polynomial f(x) with all its coefficients between 0 and p-1 inclusively, where p is a prime number, is called that f(x) is in the polynomial ring
defined on field Zp. Note that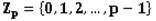 . Such a polynomial ring is called Zp[x].
. Such a polynomial ring is called Zp[x].
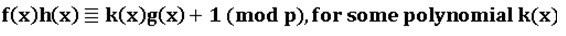
Then h(x) is called a multiplicative inverse of f(x), defined on the quotient ring Zp[x]/(g(x)). YY wonders if such an inverse always exists and is unique.
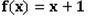 and
and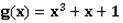 on a piece of paper.
on a piece of paper. YY noticed that 3 is a prime. Besides, he found that f(x) has a degree strictly less than g(x). And all coefficients of the two polynomials are between 0 and 2,
inclusively. His most important discovery is, that there is a polynomial
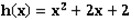 , such that
, such that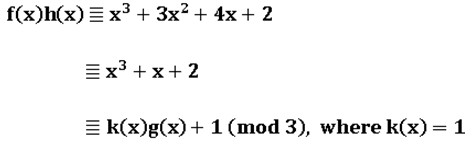
Then YY added a restriction: all coefficients of h(x) must be between 0 and 2 inclusively, and its degree must be less than g(x). Finally, he found that the polynomial
h(x) with such properties is unique.
The property that a polynomial f(x) with all its coefficients between 0 and p-1 inclusively, where p is a prime number, is called that f(x) is in the polynomial ring
defined on field Zp. Note that
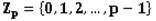 . Such a polynomial ring is called Zp[x].
. Such a polynomial ring is called Zp[x].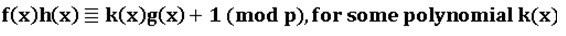
Then h(x) is called a multiplicative inverse of f(x), defined on the quotient ring Zp[x]/(g(x)). YY wonders if such an inverse always exists and is unique.
Input
Input contains multiple test cases.
For each test case, the first line contains a prime number p.
The following line consists of two positive integers n and m (n<m), indicating the degrees of f(x) and g(x).
The following line contains n+1 integers, a0, a1¡ an, indicating the coefficients of f(x), i.e.,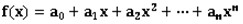 . It is guaranteed that f(x) is
. It is guaranteed that f(x) is
in Zp[x] and an¡Ù0.
The following line contains m+1 integers, b0, b1¡ bm, indicating the coefficients of g(x), i.e.,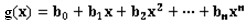 . It is guaranteed that g(x)
. It is guaranteed that g(x)
is in Zp[x] and bm¡Ù0.
Input ends with a line where p=0.
For each test case, the first line contains a prime number p.
The following line consists of two positive integers n and m (n<m), indicating the degrees of f(x) and g(x).
The following line contains n+1 integers, a0, a1¡ an, indicating the coefficients of f(x), i.e.,
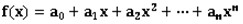 . It is guaranteed that f(x) is
. It is guaranteed that f(x) isin Zp[x] and an¡Ù0.
The following line contains m+1 integers, b0, b1¡ bm, indicating the coefficients of g(x), i.e.,
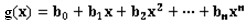 . It is guaranteed that g(x)
. It is guaranteed that g(x)is in Zp[x] and bm¡Ù0.
Input ends with a line where p=0.
Output
For each test case, if the multiplicative inverse of f(x) (defined on Zp[x]/(g(x))) does not exist, output only one line containing ¡°NO SOLUTION¡±(quotes excluded);
if the multiplicative inverse is not unique, output only one line containing ¡°NO UNIQUE SOLUTION¡±(quotes excluded). Otherwise, you should output two lines
indicating the unique multiplicative inverse h(x), using the same format as in the input.
if the multiplicative inverse is not unique, output only one line containing ¡°NO UNIQUE SOLUTION¡±(quotes excluded). Otherwise, you should output two lines
indicating the unique multiplicative inverse h(x), using the same format as in the input.
Sample Input
2 1 2 0 1 0 0 1 3 1 3 1 1 1 1 0 1 0
Sample Output
NO SOLUTION 2 2 2 1
Hint
The variable x in a polynomial can be evaluated as anything satisfying the commutative and the associative laws and having the modular p operation, not only
members of Zp. So polynomials x2+x and 0 in Z2[x] are different.
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 02:35:18, Gzip enabled |
Administration |