
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Network
Time Limit: 2000/10000 MS (Java/Others) Memory Limit: 98304/98304 K (Java/Others)Total Submission(s): 163 Accepted Submission(s): 3
Problem Description
There is a network which is a completely binary tree. In the network, there are 2N users numbered from 1, 2, 3, 4, ... 2N, which are the leaves in the network-tree. For example, Figure 1 is a network-tree. In the tree, there are 8 users (leaf nodes) and 7 transmitters (gray nodes).
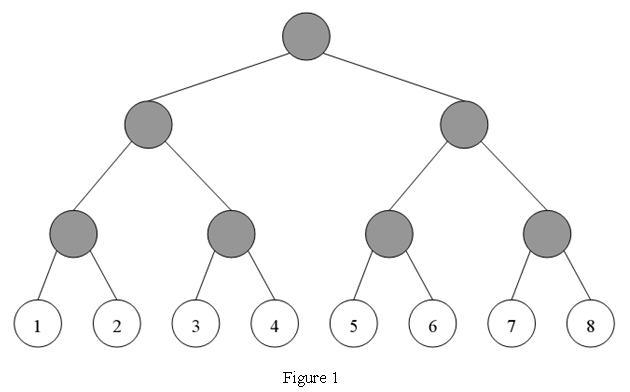
Using network-tree means that you have to pay a cost for it. The charging way is so interesting, named "pair charging". The cost you must pay is the sum of cost from every pair of user i and user j ( 1 ¡Ü i < j ¡Ü 2N). Every user can choose mode A or mode B to pay for the charge.
For every two users i, j (1 ¡Ü i < j ¡Ü 2N), first find their LCA (The Least Common Ancestors): Transmitter P. Then count the number of mode A users in the tree of ROOT transmitter P, so do mode B.
Next, let's name the number nA and nB and at last charge the cost.
f[i][j] is the flow between user i and user j.
The charging way is followed:
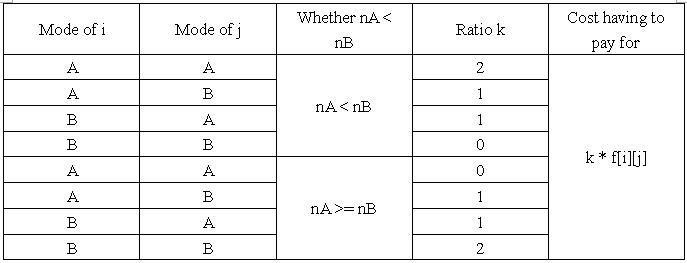
At first, every user has an initial mode, A or B. However, they want to reduce the cost, so a part of them would change the mode from A to B, or from B to A. Every change will have an extra cost. If user i changes his mode, he will pay Ci cost.
Now, you should find the minimum cost, that is, the sum of the cost having to pay for and the extra cost of changing mode.

Using network-tree means that you have to pay a cost for it. The charging way is so interesting, named "pair charging". The cost you must pay is the sum of cost from every pair of user i and user j ( 1 ¡Ü i < j ¡Ü 2N). Every user can choose mode A or mode B to pay for the charge.
For every two users i, j (1 ¡Ü i < j ¡Ü 2N), first find their LCA (The Least Common Ancestors): Transmitter P. Then count the number of mode A users in the tree of ROOT transmitter P, so do mode B.
Next, let's name the number nA and nB and at last charge the cost.
f[i][j] is the flow between user i and user j.
The charging way is followed:

At first, every user has an initial mode, A or B. However, they want to reduce the cost, so a part of them would change the mode from A to B, or from B to A. Every change will have an extra cost. If user i changes his mode, he will pay Ci cost.
Now, you should find the minimum cost, that is, the sum of the cost having to pay for and the extra cost of changing mode.
Input
First line, an integer N (N ¡Ü 10).
Sencond line, 2N integers, ith integer stands for ith user's initial mode. 0 is mode A, 1 is mode B.
Third line, 2N integers, ith integer stands for Ci, the cost that ith user changes his mode. (0 ¡Ü Ci ¡Ü 500 000)
Next 2N - 1 line, describe the flow of every pair of users. The i + 3 th line's (in the whole input) j row's integer standing for the f[i][j + i]. (1 ¡Ü i ¡Ü 2^N ,1 ¡Ü j ¡Ü 2^N - i, 0 ¡Ü f[i][j] ¡Ü 500).
Sencond line, 2N integers, ith integer stands for ith user's initial mode. 0 is mode A, 1 is mode B.
Third line, 2N integers, ith integer stands for Ci, the cost that ith user changes his mode. (0 ¡Ü Ci ¡Ü 500 000)
Next 2N - 1 line, describe the flow of every pair of users. The i + 3 th line's (in the whole input) j row's integer standing for the f[i][j + i]. (1 ¡Ü i ¡Ü 2^N ,1 ¡Ü j ¡Ü 2^N - i, 0 ¡Ü f[i][j] ¡Ü 500).
Output
Only a single integer, standing for the minimum cost above.
Sample Input
2 1 0 1 0 2 2 10 9 10 1 2 2 1 3
Sample Output
8 Explanation: Changing the user 1's mode from B to A will minimumize the cost.
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 21:38:05, Gzip enabled |
Administration |