
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Rotating a Frame
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 174 Accepted Submission(s): 54
Problem Description
Suppose you have an ice hockey ball (Which has the shape of a cylinder as shown in the figure) and a photo frame (a rectangle). You place the ball in one corner of the photo frame and keep the balls position and orientation fixed. Now you start rotating the frame in clockwise direction. But as the sides of the frame and of the ball have high friction so while the frame is rotating its surface and the balls surface never slips. So the frame always has a constant angular velocity as well as a tangential velocity as shown in the figure below.
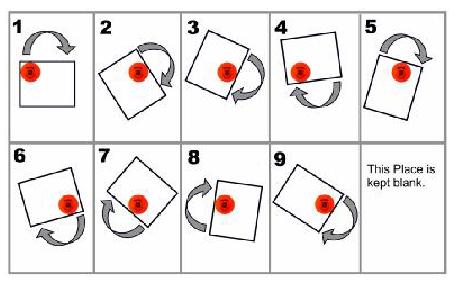
Write a program to find the position of the frame after certain time.

Write a program to find the position of the frame after certain time.
Input
he input contains several test cases. Each set of input is contained in two lines. The first line of a set contains eight integers which denote the values x1, y1, x2, y2, x3, y3 and x4, y4 respectively. These values indicate that the four vertices of the frame in clockwise order are denoted by the Cartesian coordinates P1 (x1, y1) , P2 (x2, y2) , P3 (x3, y3) and P4 (x4, y4) . You can assume that 0<=| x1|,| y1|,| x2|,| y2|,| x3|,| y3|,| x4|,| y4|<=1000 . The second line contains three floating point numbers which denotes the values of R (0 < R < 1000) , T (0<=T < 100000) and 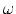 (0<=
(0<= 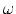 < 360) respectively. Here R is the radius of the ice hockey ball, T denotes that we want to know the position of the frame after T seconds and
< 360) respectively. Here R is the radius of the ice hockey ball, T denotes that we want to know the position of the frame after T seconds and 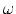 is the angular velocity of the frame in degree/second. You can assume that ball is placed touching two the si! des that intersect at point (x1, y1) and it never moves from or rotates in that position. There will be no such input where the hockey ball cannot be placed within the frame. The last test case is followed by a single zero, which should not be processed.
is the angular velocity of the frame in degree/second. You can assume that ball is placed touching two the si! des that intersect at point (x1, y1) and it never moves from or rotates in that position. There will be no such input where the hockey ball cannot be placed within the frame. The last test case is followed by a single zero, which should not be processed.
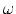 (0<=
(0<= 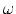 < 360) respectively. Here R is the radius of the ice hockey ball, T denotes that we want to know the position of the frame after T seconds and
< 360) respectively. Here R is the radius of the ice hockey ball, T denotes that we want to know the position of the frame after T seconds and 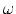 is the angular velocity of the frame in degree/second. You can assume that ball is placed touching two the si! des that intersect at point (x1, y1) and it never moves from or rotates in that position. There will be no such input where the hockey ball cannot be placed within the frame. The last test case is followed by a single zero, which should not be processed.
is the angular velocity of the frame in degree/second. You can assume that ball is placed touching two the si! des that intersect at point (x1, y1) and it never moves from or rotates in that position. There will be no such input where the hockey ball cannot be placed within the frame. The last test case is followed by a single zero, which should not be processed. Output
For each test case, print the case number and eight floating point numbers x1f, y1f, x2f, y2f, x3f, y3f, x4f and y4f , to three decimal places. These floating-point numbers actually denote the final positions of the points (x1, y1),(x2, y2),(x3, y3) and (x4, y4) (The four corners of the frame) respectively after time T seconds.
Sample Input
0 1 1 1 1 0 0 0 0.2 10 0 0 1 1 1 1 0 0 0 0.2 10 100 0
Sample Output
Case 1: 0.000 1.000 1.000 1.000 1.000 0.000 0.000 0.000 Case 2: -0.619 0.132 -0.445 1.117 0.539 0.943 0.366 -0.042
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 17:22:20, Gzip enabled |
Administration |