Pusher

PusherBoy is an online game http://www.hacker.org/push . There is an R * C grid, and there are piles of blocks on some positions. The goal is to clear the blocks by pushing into them.

You should choose an empty area as the initial position of the PusherBoy. Then you can choose which direction (U for up, D for down, L for left and R for right) to push. Once the direction is chosen, the PusherBoy will walk ahead until he met a pile of blocks (Walking outside the grid is invalid). Then he remove one block from the pile (so if the pile contains only one block, it will become empty), and push the remaining pile of blocks to the next area. (If there have been some blocks in the next area, the two piles will form a new big pile.)

Please note if the pusher is right up against the block, he can't remove and push it. That is, there must be a gap between the pusher and the pile. As the following figure, the pusher can go up, but cannot go down. (The cycle indicates the pusher, and the squares indicate the blocks. The nested squares indicate a pile of two blocks.)


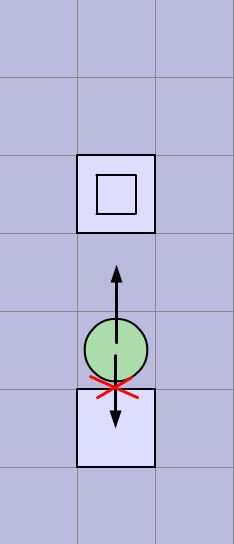
And if a whole pile is pushed outside the grid, it will be considered as cleared.

There are several test cases in each input. The first two lines of each case contain two numbers C and R. (R,C <= 25) Then R lines follow, indicating the grid. '.' stands for an empty area, and a lowercase letter stands for a pile of blocks. ('a' for one block, 'b' for two blocks, 'c' for three, and so on.)

Output three lines for each case. The first two lines contains two numbers x and y, indicating the initial position of the PusherBoy. (0 <= x < R, 0 <= y < C). The third line contains a moving sequence contains 'U', 'D', 'L' and 'R'. Any correct answer will be accepted.

3
7
...
...
.b.
...
...
.a.
...

4
1
UDU
[center][img]../../../data/images/2821-2.jpg[/img][/center] 

Hint: The following figures show the sample. The circle is the position of the pusher.
And the squares are blocks (The two nested squares indicating a pile of two blocks). And this is the unique solution for this case.

2009 Multi-University Training Contest 1 - Host by TJU