
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Hyperspace
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 606 Accepted Submission(s): 65
Problem Description
Hyperspace ,A Euclidean space of dimension greater than three (the original meaning of the word hyperspace, common in late nineteenth century British books, sometimes used in paranormal context, but which has become rarer since then). Minkowski space, a concept, often referred to by science fiction writers as hyperspace that refers to the four-dimensional space-time of special relativity.

Here we define a “Hyperspace” as a set of points in three-dimensional space. We define a function to describe its “Hyperspace Value”
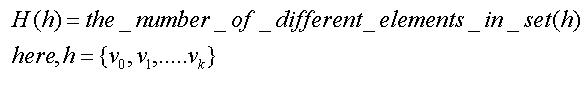
Every vi (0<=i<=k) could be describe in three-dimensional reference system, say v0 (1, 2, 3)
For the following question, we will have to deal with the “Hyperspaces”, you may assume that the number of “Hyperspace” is always no larger than 100.
As we say above, we give every “Hyperspace” an “ID” to identify it.
If you want to connect two points in two different “Hyperspaces”, it will cost you F to build the connection. F can be defined as the following expression:

In addition, you can only create at most one connection between any two “Hyperspaces”.
If you want to connect two points in the same “Hyperspaces” whose “ID” is k, it will cost you G to build the connection. G can be defined as the following expression:
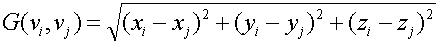
Here
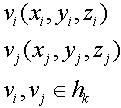
Now your task is quite easy.
AekdyCoin gives you n “Hyperspaces”.
Then he gives you information about all the points in the “Hyperspaces”
Now he wants to know the minimal cost to connect all the points in all “Hyperspaces”
you have to ensure that any two different points in the same "Hyperspace" could be connected directly or indirectly by the connections you build in this "Hyperspace".


Here we define a “Hyperspace” as a set of points in three-dimensional space. We define a function to describe its “Hyperspace Value”
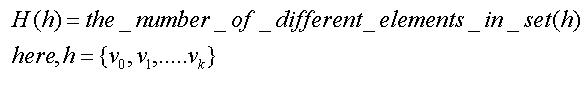
Every vi (0<=i<=k) could be describe in three-dimensional reference system, say v0 (1, 2, 3)
For the following question, we will have to deal with the “Hyperspaces”, you may assume that the number of “Hyperspace” is always no larger than 100.
As we say above, we give every “Hyperspace” an “ID” to identify it.
If you want to connect two points in two different “Hyperspaces”, it will cost you F to build the connection. F can be defined as the following expression:

In addition, you can only create at most one connection between any two “Hyperspaces”.
If you want to connect two points in the same “Hyperspaces” whose “ID” is k, it will cost you G to build the connection. G can be defined as the following expression:
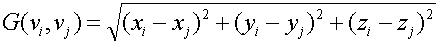
Here
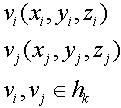
Now your task is quite easy.
AekdyCoin gives you n “Hyperspaces”.
Then he gives you information about all the points in the “Hyperspaces”
Now he wants to know the minimal cost to connect all the points in all “Hyperspaces”
you have to ensure that any two different points in the same "Hyperspace" could be connected directly or indirectly by the connections you build in this "Hyperspace".
Input
The input consists of several test cases.
In the first line there is an integer n (1<=n<=100), indicating the number of “Hyperspaces”
Then follow an integer m (1<=m<=100000)
You can assume that the number of different points in every “Hyperspace” is always no larger than 100.
The next m lines contain the descriptions of all the points
All the descriptions are given in the following format x,y,z,id
Indicating the point (x,y,z) belongs to the id “Hyperspace”
id is an integer.
x,y,z are all real number with at most four fractional digits.
-10000<=x,y,z<=10000,1<=id<=n
In the first line there is an integer n (1<=n<=100), indicating the number of “Hyperspaces”
Then follow an integer m (1<=m<=100000)
You can assume that the number of different points in every “Hyperspace” is always no larger than 100.
The next m lines contain the descriptions of all the points
All the descriptions are given in the following format x,y,z,id
Indicating the point (x,y,z) belongs to the id “Hyperspace”
id is an integer.
x,y,z are all real number with at most four fractional digits.
-10000<=x,y,z<=10000,1<=id<=n
Output
For each test case, output the minimal cost on a single line.
Please round it to four fractional digits.
Please round it to four fractional digits.
Sample Input
1 2 1 2 1 1 1 3 1 1
Sample Output
1.0000
Author
AekdyCoin
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.001000(s) query 1, Server time : 2025-04-01 06:54:46, Gzip enabled |
Administration |