
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
TCE-frep number system
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 531 Accepted Submission(s): 135
Problem Description
Number theory is one of the oldest branches of pure mathematics, and one of the largest. Of course, it concerns questions about numbers, usually meaning whole numbers or rational numbers (fractions).
Elementary number theory involves divisibility among integers -- the division "algorithm", the Euclidean algorithm (and thus the existence of greatest common divisors), elementary properties of primes (the unique factorization theorem, the infinitude of primes), congruences, including Fermat's little theorem and Euler's theorem extending it. But the term "elementary" is usually used in this setting only to mean that no advanced tools from other areas are used -- not that the results themselves are simple.
Topics in elementary number theory -- the solutions of sets of linear congruence equations (the Chinese Remainder Theorem), or solutions of single binary quadratic equations (Pell's equations and continued fractions), or the generation of Fibonacci numbers or Pythagorean triples -- turn out in retrospect to be harbingers of sophisticated tools and themes in other areas. The remaining parts of number theory are more or less closely allied with other branches of mathematics, and typically use tools from those areas.
Also there lots of branches, such as Combinatorial Number Theory, Algebraic Number Theory, Analytic Number Theory, additive number theory, Geometric number theory, Transcendental number theory, etc.
Today give you a function g(n) whose value is the sum of all the divisors of n .
If n satisfies following rule:
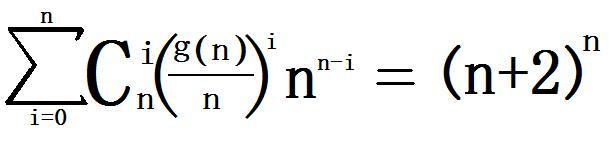
We call n is a TCE-frep number,your task is easy,detail to input and output.
Elementary number theory involves divisibility among integers -- the division "algorithm", the Euclidean algorithm (and thus the existence of greatest common divisors), elementary properties of primes (the unique factorization theorem, the infinitude of primes), congruences, including Fermat's little theorem and Euler's theorem extending it. But the term "elementary" is usually used in this setting only to mean that no advanced tools from other areas are used -- not that the results themselves are simple.
Topics in elementary number theory -- the solutions of sets of linear congruence equations (the Chinese Remainder Theorem), or solutions of single binary quadratic equations (Pell's equations and continued fractions), or the generation of Fibonacci numbers or Pythagorean triples -- turn out in retrospect to be harbingers of sophisticated tools and themes in other areas. The remaining parts of number theory are more or less closely allied with other branches of mathematics, and typically use tools from those areas.
Also there lots of branches, such as Combinatorial Number Theory, Algebraic Number Theory, Analytic Number Theory, additive number theory, Geometric number theory, Transcendental number theory, etc.
Today give you a function g(n) whose value is the sum of all the divisors of n .
If n satisfies following rule:
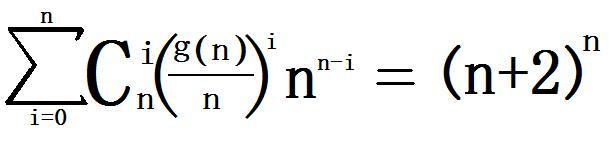
We call n is a TCE-frep number,your task is easy,detail to input and output.
Input
Two ways of input:
A x y
(x, y <= 2^63-1)
Q n
(1 <= n <= 2^63-1)
A x y
(x, y <= 2^63-1)
Q n
(1 <= n <= 2^63-1)
Output
For A x y , output the number of TCE-frep number which located between x and y
For Q n , output “1” if n is a TCE-frep number else output “0”
For Q n , output “1” if n is a TCE-frep number else output “0”
Sample Input
A 5 70 A 6 6 Q 6 Q 1
Sample Output
2 1 1 0
Author
WhereIsHeroFrom
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2025-03-30 10:20:20, Gzip enabled |
Administration |