
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
棋盘分割
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 772 Accepted Submission(s): 391
Problem Description
将一个8*8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了(n-1)次后,连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)
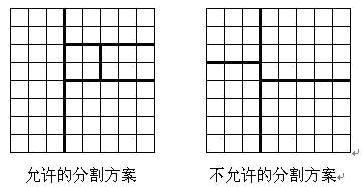
原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差
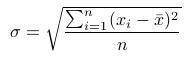
,其中平均值
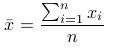
xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n,求出O'的最小值。

原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差
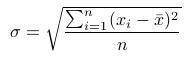
,其中平均值
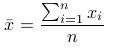
xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n,求出O'的最小值。
Input
第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
Output
仅一个数,为O'(四舍五入精确到小数点后三位)。
Sample Input
3 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 3
Sample Output
1.633
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 11:05:50, Gzip enabled |
Administration |