
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Minimal Ratio Tree
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 6112 Accepted Submission(s): 2012
Problem Description
For a tree, which nodes and edges are all weighted, the ratio of it is calculated according to the following equation.
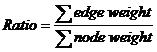
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
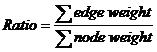
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
Input
Input contains multiple test cases. The first line of each test case contains two integers n (2<=n<=15) and m (2<=m<=n), which stands for the number of nodes in the graph and the number of nodes in the minimal ratio tree. Two zeros end the input. The next line contains n numbers which stand for the weight of each node. The following n lines contain a diagonally symmetrical n¡Án connectivity matrix with each element shows the weight of the edge connecting one node with another. Of course, the diagonal will be all 0, since there is no edge connecting a node with itself.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.
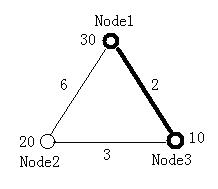
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.

Output
For each test case output one line contains a sequence of the m nodes which constructs the minimal ratio tree. Nodes should be arranged in ascending order. If there are several such sequences, pick the one which has the smallest node number; if there's a tie, look at the second smallest node number, etc. Please note that the nodes are numbered from 1 .
Sample Input
3 2 30 20 10 0 6 2 6 0 3 2 3 0 2 2 1 1 0 2 2 0 0 0
Sample Output
1 3 1 2
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-25 16:16:30, Gzip enabled |
Administration |