
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Minimal search cost
Time Limit: 10000/4000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 522 Accepted Submission(s): 187
Problem Description
As we know, we need to spend O(n) time in the abstract finding a key(every two keys are different) in a non-sorted array. But if we make up a BST(binary search tree) before, then for each access, you need to spend log(N) time to do it. And for each access, there exists a road from the root node to the target node, whose length Ci is the number of the edges of the road.
Because there is an accessing frequency Fi for each key. And the total value of the tree is defined as following rule: SUM=Sigma(Ci*Fi), for i from 0 to N-1, N is the number of the keys. You need to find the minimal value M_SUM to make up a tree.

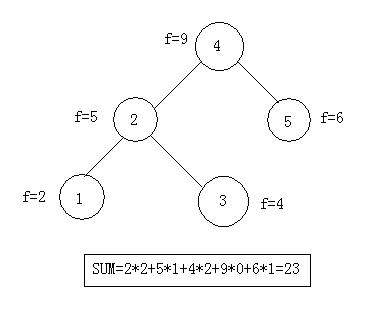
Because there is an accessing frequency Fi for each key. And the total value of the tree is defined as following rule: SUM=Sigma(Ci*Fi), for i from 0 to N-1, N is the number of the keys. You need to find the minimal value M_SUM to make up a tree.


Input
There are a lot of cases. In each case, in the first line, there is an integer N to represent the number of keys. In the second line, there are N sorted integers Ki. In the third line, there are N integers Fi, which are the accessing frequency. 0<N<=1000, 0<=Fi<65536.
Output
For each case, just output the minimal search cost.
Sample Input
5 1 2 3 4 5 2 5 4 9 6
Sample Output
23
Author
wangye
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 11:38:41, Gzip enabled |
Administration |