
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Fermat vs. Pythagoras
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 258 Accepted Submission(s): 97
Problem Description
Computer generated and assisted proofs and verification occupy a small niche in the realm of Computer Science. The first proof of the four-color problem was completed with the assistance of a computer program and current efforts in verification have succeeded in verifying the translation of high-level code down to the chip level.
This problem deals with computing quantities relating to part of Fermat's Last Theorem: that there are no integer solutions of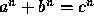 for n > 2.
for n > 2.
Given a positive integer N, you are to write a program that computes two quantities regarding the solution of

where x, y, and z are constrained to be positive integers less than or equal to N. You are to compute the number of triples (x,y,z) such that x<y< z, and they are relatively prime, i.e., have no common divisor larger than 1. You are also to compute the number of values 0<p≤n such that p is not part of any triple (not just relatively prime triples).
This problem deals with computing quantities relating to part of Fermat's Last Theorem: that there are no integer solutions of
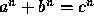 for n > 2.
for n > 2. Given a positive integer N, you are to write a program that computes two quantities regarding the solution of

where x, y, and z are constrained to be positive integers less than or equal to N. You are to compute the number of triples (x,y,z) such that x<y< z, and they are relatively prime, i.e., have no common divisor larger than 1. You are also to compute the number of values 0<p≤n such that p is not part of any triple (not just relatively prime triples).
Input
The input consists of a sequence of positive integers, one per line. Each integer in the input file will be less than or equal to 1,000,000. Input is terminated by end-of-file.
Output
For each integer N in the input file print two integers separated by a space. The first integer is the number of relatively prime triples (such that each component of the triple is <=N ). The second number is the number of positive integers <=N that are not part of any triple whose components are all <=N . There should be one output line for each input line.
Sample Input
10 25 100
Sample Output
1 4 4 9 16 27
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2025-04-01 07:06:03, Gzip enabled |
Administration |