Problem F
Time Limit : 6000/3000ms (Java/Other) Memory Limit : 131072/131072K (Java/Other)
Total Submission(s) : 85 Accepted Submission(s) : 36
Font: Times New Roman | Verdana | Georgia
Font Size: ← →
Problem Description
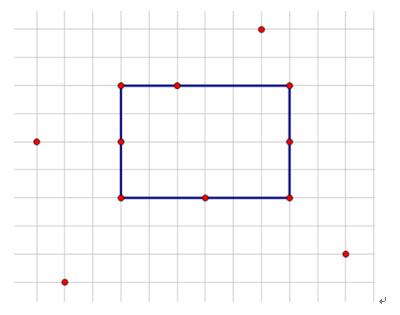
There are n points in a geometrical plane. If there exists a rectangle whose four vertices are among those points and every edge of the rectangle has exactly m points which are among those points, now ask how many rectangles existing in this plane could satisfy all the conditions. The edge of the rectangle should be parallel to the coordinate axes. This is a rectangle that satisfy the conditions when m=3 represented in the chart below.

Input
First line contains $T (T \leq 20)$ denoting the number of test cases.
$T$ cases follows for each cases:
First line contains two integers $n, m (5\leq n \leq 100000, m < n)$
Followed by $n$ lines, each line contains two integers $x_{i}, y_{i}$ indicates the location of the i-th point. There are no two points at the same location. $(|X_{i}|, |Y_{i}|\leq 10000000)$
$T$ cases follows for each cases:
First line contains two integers $n, m (5\leq n \leq 100000, m < n)$
Followed by $n$ lines, each line contains two integers $x_{i}, y_{i}$ indicates the location of the i-th point. There are no two points at the same location. $(|X_{i}|, |Y_{i}|\leq 10000000)$
Output
For each case, output an integer indicate the number of rectangles that satisfy the condition.
Sample Input
1 9 2 0 0 0 3 0 6 3 0 3 3 3 6 6 0 6 3 6 6
Sample Output
4
