The Tower
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total Submission(s): 548 Accepted Submission(s): 115
Special Judge
Problem Description
The Tower shows a tall tower perched on the top of a rocky mountain. Lightning strikes, setting the building alight, and two people leap from the windows, head first and arms outstretched. It is a scene of chaos and destruction.
There is a cone tower with base center at (0, 0, 0), base radius r and apex (0, 0, h). At time 0 , a point located at ($x_0$, $y_0$, $z_0$) with velocity ($v_x$, $v_y$, $v_z$). What time will they collide? Here is the cone tower.
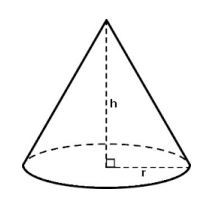
There is a cone tower with base center at (0, 0, 0), base radius r and apex (0, 0, h). At time 0 , a point located at ($x_0$, $y_0$, $z_0$) with velocity ($v_x$, $v_y$, $v_z$). What time will they collide? Here is the cone tower.

Input
The first line contains testcase number $T$ ($T$ ≤ 1000), For each testcase the first line contains spaceseparated real numbers $r$ and $h$ (1 ≤ $r$, $h$ ≤ 1000) — the base radius and the cone height correspondingly.
For each testcase the second line contains three real numbers $x_0$, $y_0$, $z_0$ (0 ≤ |$x_0$|, |$y_0$|, $z_0$ ≤ 1000). For each testcase the third line contains three real numbers $v_x$, $v_y$, $v_z$ (1 ≤ $v_x^2$ + $v_y^2$ + $v_z^2$ ≤ 3 × $10^6$). It is guaranteed that at time 0 the point is outside the cone and they will always collide.
For each testcase the second line contains three real numbers $x_0$, $y_0$, $z_0$ (0 ≤ |$x_0$|, |$y_0$|, $z_0$ ≤ 1000). For each testcase the third line contains three real numbers $v_x$, $v_y$, $v_z$ (1 ≤ $v_x^2$ + $v_y^2$ + $v_z^2$ ≤ 3 × $10^6$). It is guaranteed that at time 0 the point is outside the cone and they will always collide.
Output
For each testcase print Case $i$ : and then print the answer in one line, with absolute or relative error not exceeding $10^{-6}$
Sample Input
2 1 2 1 1 1 -1.5 -1.5 -0.5 1 1 1 1 1 -1 -1 -1
Sample Output
Case 1: 0.3855293381 Case 2: 0.5857864376
Source
642ccpc吉林
